Derivada
Derivada
Derivada
"A derivada é o coeficiente de inclinação da reta tangente ao gráfico de uma função y = f(x) em um determinado ponto P=(x0, f(x0)). Ela pode ser calculada através da fórmula:
Ou, se chamarmos x – x0 de h, podemos usar a fórmula:
Ambas as fórmulas estão corretas, mas dependendo da situação é mais conveniente usar uma ou outra.
Além da notação dx/dx, que se lê “a derivada de y em relação a x”, é muito comum utilizarmos uma linha para representála, como f'(x), que representa a derivada de f(x).
A derivada possui uma infinidade de aplicações nos ramos da Matemática, da Física e da Engenharia. Ela pode ser utilizada, por exemplo, para calcular a velocidade instantânea de um corpo ou de uma partícula em um instante t ou para resolver problemas que envolvam a variação de duas grandezas.
É interessante notar que a derivada sempre será um limite que resultará em uma situação 0/0, o que exigirá sua simplificação para alcançarmos seu verdadeiro valor. Por ser um limite, uma função apenas será diferenciável (um outro nome para derivável) em certo ponto se o limite da fórmula da derivada existir naquele ponto. De forma geral, uma função f(x) não será derivável em pontos que tenham bico ou em cuja reta tangente seja vertical. Ainda, se f(x) for diferenciável em um ponto x0, então f(x) é contínua em x0, mas a recíproca não é verdadeira!"
(clique na imagem! será redirecionado para a origem dela!)
Integral
Integral
Integral
"Integral, também conhecida como antiderivada, permite encontrar a função primitiva de uma função qualquer.
Propriedades de integração:
Da mesma forma que a adição e a subtração, a multiplicação e a divisão, a operação inversa da derivação é a antiderivação ou integração indefinida.
Dada uma função g(x), qualquer função f'(x) tal que f'(x) = g(x) é chamada integral indefinida ou antiderivada de f(x).
Exemplos:
Se , então é a derivada de f(x). Umas das antiderivadas de
f'(x) = g(x) = x^4 é .
Se f(x) = x^3, então f'(x) = 3x^2 = g(x). Umas das antiderivadas de g(x) = 3x^2 é f(x) = x^3.
Se f(x) = x^3 + 4, então 3x^2. Umas das antiderivadas de g(x) = 3x^2 é x^3 + 4.
Nos exemplos 2 e 3 podemos observar que tanto x^3 quando x^3+4 são integrais indefinidas para 3x^2. A diferença entre quaisquer destas funções (chamadas funções primitivas) é sempre uma constante, ou seja, a integral indefinida de 3x^2 é x^3+C, onde C é uma constante real.
Integral definida:
Seja uma função f(x) definida e contínua num intervalo real [a, b]. A integral definida de f(x), de a até b, é um número real, e é indicada pelo símbolo:
onde:
a é o limite inferior de integração;
b é o limite superior de integração;
f(x) é o integrando.
Se representa a área entre o eixo x e a curva f(x), para .
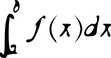

Propriedades das integradas indefinidas:
São imediatas as seguintes propriedades:
1. , ou seja, a integral da soma ou diferença é a soma ou diferença das integrais.
2. , ou seja, a constante multiplicativa pode ser retirada do
integrando.
3. , ou seja, a derivada da integral de uma função é a própria
função."
